Teori dan Contoh Ekspresi Boolean Sum of Product (SOP)

Di tulisan ini, kita akan belajar bagian dari teknik elektro, mengenai teori, langkah dan contoh penerapan ekspresi boolean Sum of Product (SOP).

Sum of Product (SOP) adalah metode untuk menentukan ekpresi boolean atau gerbang logika yang sudah diketahui tabel kebenarannya. Caranya adalah dengan menyatukan pada gerbang (Sum /OR) yang merupakan hasil dari perkalian (Product /AND). Untuk lebih jelasnya berikut contoh penggunaan ekspresi boolean SOP.

1. Diketahui tabel kebenaran dengan input A, B dan C. Maka tentukan ekspresi boolean dan gerbang logikanya.

Jawab:

A	B	C	Y
0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	0
1	0	0	0
1	0	1	0
1	1	0	0
1	1	1	1

a) Untuk menentukan ekspresi boolean, kita soroti output tabel kebenaran yang mempunyai nilai output 1.
Maka ekspresi boolean dengan metode SOP adalah dengan mengalikan (PRODUCT / AND) terlebih dahulu, selanjutnya baru dijumlahkan (SUM / OR). Sebelum dikalikan, nilai logika inputnya harus bernilai 1, apabila bernilai 0, maka diinversekan terlebih dahulu. Dan ini adalah ekpresi boolean pada tabel kebenaran diatas.

Y = (invA.invB.C) + (A.B.C)

b) Untuk gerbang logika, kita dapat menentukannya dari ekpresi boolean yang telah didapat, berikut adalag gerbang logikanya.

2. Diketahui tabel kebenaran dengan input A, B dan C. Maka tentukan ekspresi boolean dan gerbang logikanya.

Jawab:

A	B	C	Y
0	0	0	1
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	0
1	1	1	0

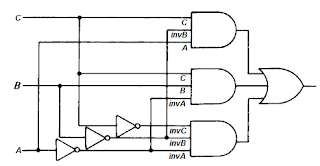
a) Ekspresi Boolean

Y = (invA.invB.invC)+(invA.B.C)+(A.invB.C)

b) Gerbang Logika